ディープラーニングのしくみがわかる数学入門
超基本
賢い動作とは
- 今までのシステムは、データを人間が読んでルールを導く。
- これからのシステムは、人工知能がデータを読んでルールを導く。
交差検証
訓練データと検証データ(テストデータ)を入れ替えることで、精度を確認すること。例えば、ランダムに選んだり、偶数日のデータを訓練データ・奇数日のデータをテストデータにするなど。
最適化問題
(例えば正解率などが)最大や最小となる状態を求める問題のこと。
効率的な探索
最適化問題では、データ量が増えても短い時間で探索する必要があり、以下のような探索方法が使われる。
- 単純増加する関数 → 二分探索など
- ランダムに変化する関数 → 遺伝的アルゴリズムなど
機械学習の考え方
関数 --- 入力を受け取り、何らかの変換を行い、出力する。ブラックボックスのようなもの。
機械学習の種類
- 教師あり学習
- 個々のデータが「入力」と「正しい出力」のペアとなるようにする
- データを「訓練用」と「テスト用」に分ける
- コンピュータに、訓練用データで学習させ、関数を作らせる
- 作った関数でテスト用データを処理したときに正解率が高くなるよう、何度も調整してやり直す(どの関数を使うか、パラメータをどう調整するかなど)
- 教師なし学習
- 正解がわからない場合、正解を用意できない場合に使う
- データの特徴を掴むために使う(クラスタリングなど)
- 強化学習
- 報酬が最大になるよう、コンピュータに試行錯誤で学習させる
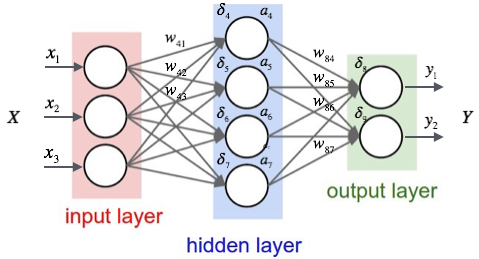
ニューラルネットワーク
- 人工知能を実現する一つの方法が機械学習
- 機械学習を実現する一つの方法がニューラルネットワーク
- ニューラルネットワークを進化させたのがディープラーニング
動作
- ニューロンは入力(=信号)とその「重み」を受け取る。
- 結果がしきい値を超えたら 1 を出力する(発火する)。超えなければ 0 を出力する。
- 入力層、中間層、出力層を持つ
- 上記図の場合、重みを持つ層が 2 層なので、2 層ネットワークと呼ぶ。中間層が増えれば、3 層、4 層・・・ネットワークという。
- まずはじめは、重みはランダムに設定される。その後、訓練データを入れて、正しい結果が得られるよう重みを調整する(最適化、学習などという)。
- テストデータで正解率を求めて、そのネットワークを評価する
- 訓練データにのみ最適化したネットワークができてしまう過学習が起こらないよう、あえて最適化を制限する場合もある
数列・統計・確率
数列と集合
数列、漸化式
- 数列 --- 数が一列に並んでいるもの。順番に意味がある。
- 項 --- 一つの数。初項、第 2 項、第 3 項、、、第項(一般項)
- 一般項 --- 第項の値を、の値だけを使って記述した式
- 漸化式 --- 第項の値を、複数の項の関係で記述した式(フィボナッチ数列など)
漸化式は、プログラムのループ処理で書くと簡単。一方、漸化式を一般項に変換するのは難しい場合が多い。
数列の和
数列の和は大文字シグマで表される。初項から第項までの和()は、下記の式で表される。
数列の和はループ処理で求めてもよいが、公式を活用するとより高速に処理できる。
集合、内包表記
- 集合 --- 数の集まり。順番に意味がない。 など、大文字アルファベットで表す。
- 有限集合 --- など限りがある集合
- 無限集合 ---
整数など限りがない集合。{n|nは整数}などの表現をする。
平均、分散、標準偏差
| 名前 | 表現 | 説明 |
|---|---|---|
| 算術平均 | NumPy ではmean、こちらを使うことが多い | |
| 加重平均 | NumPy ではaverage | |
| 分散(Variance) | 「平均との差の 2 乗」の総計 | |
| 標準偏差(Standard Deviation) | 分散の平方根 |
※ 分散・標準偏差は小文字のシグマで表す
データの標準化(Z スコア正規化)
平均を 0、分散を 1 に合わせること。標準化された各データ()は、下記の式で求めることができる。
- --- 標準化前の各データ
- --- 平均
- --- 標準偏差
データの分布
データの分布を考えることはとても大切。ヒストグラム(度数分布表)などを使う。
- 正規分布(normal distribution)
- 一様分布(uniform distribution)
- 二項分布(binomial distribution)
確率
確率の基本
「試行」を行い「事象」が起こる。
事象 A が起こる確率 = 事象 A が起こるパターン数 / 試行によって起こりうる全パターン数
事象 A が起こる確率をと表す。
- 数学的確率 --- 計算で求めた確率
- 統計的確率 --- 実際に試行して求めた確率
確率変数と確率分布
- 確率変数()
- 確率的に決まる値のこと。確率に従っていろいろな値をとる変数のこと。
- 離散型と連続型がある
- e.g. サイコロを振ったときに出る目は、確率変数である
- 確率分布
- 「確率変数の取りうる値」と「その値をとる確率」の対応のこと
- 離散型では表(確率分布表という)で、連続型ではグラフで表現することが多い
確率によって値が変動するものを「確率変数 」とおき、その確率分布を調べることで、さまざまな物事を「確率による重み」をつけて計算することが可能になる
確率分布表の例
| 確率変数 | ... | ||||
| 確率 | ... |
確率変数の期待値(expected value)
確率変数の期待値 = 確率変数の平均値
離散型の場合は下記の式で計算する。
連続型確率変数の場合は積分により計算する(省略)。
期待値の性質
は定数、は確率変数
- ※が独立でない場合でも成り立つ
確率変数の分散
離散型の場合は下記の式で計算する。
連続型確率変数の場合は積分により計算する(省略)
なお、下記の公式を使えば、分散を期待値から算出することができる。
分散の性質
は定数、は確率変数
- ※が独立である場合のみ成り立つ
独立
複数の事象が互いに独立である、とは、ある事象が他の事象に影響しないこと
同時確率
独立した 2 つの事象 がある時、
- これらが同時に起こる事象を、事象 の積事象といい、 と表す。
- これらが同時に起こる確率を同時確率といい、 と表す。
同時確率は下記の通り計算する。
条件付き確率
独立していない事象があり、事象が起こることが確定しているときに、事象が起こる確率のこと。 Venn diagram で考えるとわかりやすい。
以下、
- :時系列的に先に位置する確率変数(条件、原因)
- :時系列的に後に位置する確率変数(結果)
として表記する。
上記のように、条件付き確率では、原因(≒ 条件)を右側に記載する。
P(Bである確率|Aであったとき)
確率の乗法定理
独立していない事象があるとき、事象が続けて起こる確率を計算するには、先の式を変形させて導いた「確率の乗法定理」をつかう。
ベイズの定理
条件付き確率に関する定理の一つ。通常は「原因」から「結果」を探るのに対し、「結果」から「原因」を逆方向に探りたいときに、ベイズの定理を使う。
- --- 事前確率 まだ何も情報がないときに、既に知っている確率のこと
- --- 事後確率 という情報が後から加わる事により、である確率をより絞りんだもの
例)罹患率 0.01%の病気の検査の精度が以下の場合において、陽性と診断されたときに本当に罹患している確率は?
| 陽性 | 陰性 | |
|---|---|---|
| 罹患 | 98% | 2% |
| 非罹患 | 20% | 80% |
- 罹患しているとき(原因)に、陽性と判断される(結果)可能性 => 条件付き確率
- 陽性と判断された(結果)ときに、罹患している(原因)可能性 => ベイズの定理
P(罹|陽) = { P(陽|罹)\*P(罹) } / P(陽)
P(陽|罹) = 0.98
P(罹) = 0.0001
P(陽) = (0.0001 * 0.98) + (0.9999 * 0.20)
P(罹|陽) = 0.05 %
大量のデータから推定する
標本と推定
- 母集団 --- すべてのデータ
- 標本 --- 母集団から抽出した一部のデータ
- 推定 --- 標本を使って母集団の平均や分散を推測すること
- 点推定 --- 標本の平均も、母集団の平均も、同じだとみなす考え方
中心極限定理
「どんな分布でも標本平均の分布は正規分布である」
平均、分散の母集団があるとき、母集団から「個の標本」を「繰り返し」取り出したとき、標本平均(標本の値の総計/標本数)の分布は、平均、分散の正規分布に近づく。
が大きくなるほど、標準正規分布に近づく。
これは、母集団の分布がどのような種類であっても成り立つ。
中心極限定理を活用すると、母集団の分布の種類や、母平均(母集団の平均)がわからなくても、「個の標本」を「たくさん」集めることで、「母平均は 95%の確率で**から**の間にあります」と主張できるようになる。
https://www.youtube.com/watch?v=CHOLN1tAJWI
正規分布のパーセント点
正規分布の端を ○%除く場合の標準偏差の値を「%点」という。5%点は一番よく使う。
| 両側 | 片側 | パーセント点 |
|---|---|---|
| 1%点 | 0.5%点 | -2.58, 2.58 |
| 5%点 | 2.5%点 | -1.96, 1.96 |
| 10%点 | 5%点 | -1.64, 1.64 |
一様乱数と正規乱数
- 一様乱数
- 0 から 1 までの値が均等に出現するように生成される乱数
- 標本の抜き出し等に使う
- 正規乱数
- 平均が 0,標準偏差が 1 となるように生成される乱数
- ニューラルネットワークの重み付けの初期値等に使う
確率分布の推定
機械学習においては母集団の分布は分からないので、「分布の推定」が必要
- ノンパラメトリックな手法 --- 一切の分布を仮定しない方法
- パラメトリックな手法 --- データが何らかの分布に従うと仮定する方法
- 最尤(さいゆう)推定
- ベイズ推定
複数の入出力をまとめて処理する
用語
- スカラー
- 大きさのみを表す量
- など
- ベクトル・ベクター
- 大きさと向きを持つ量
- など、太字のアルファベットで表現する。
ベクトルの表現
座標軸の数だけ並べて記述する。x,y,z の順などが一般的。
- 横ベクトル・行ベクトルでの表記
- 縦ベクトル、列ベクトルの場合
行列
ベクトルの表現は 1 行 or1 列だが、縦横方向にデータを並べたものを行列という。
用語
- スカラー 0 次元
- ベクトル 1 次元
- 行列 2 次元
- テンソル 多次元
ベクトルの和
の和は
ベクトルの大きさ
の大きさは下記のように表す。
ベクトルの内積
- の大きさに、が作る影の大きさを掛け合わせたもの
- 直角なら 0、反対方向ならマイナスの値になる
numpy だと下記のように計算できる。
a = np.array([2, 1])
b = np.array([-1, 2])
print(a.dot(b)) # => 0 (直角だから)
コーシー・シュワルツの不等式
- 内積の最大値は、が同じ向きのとき
- 内積の最小値は、が反対向きのとき